nonhermitian

M3

3 min read

Matrix-free Measurement Mitigation (M3)

Collaborators

Hwajung Kang, Neereja Sundaresan, and Jay M. Gambetta

Summary

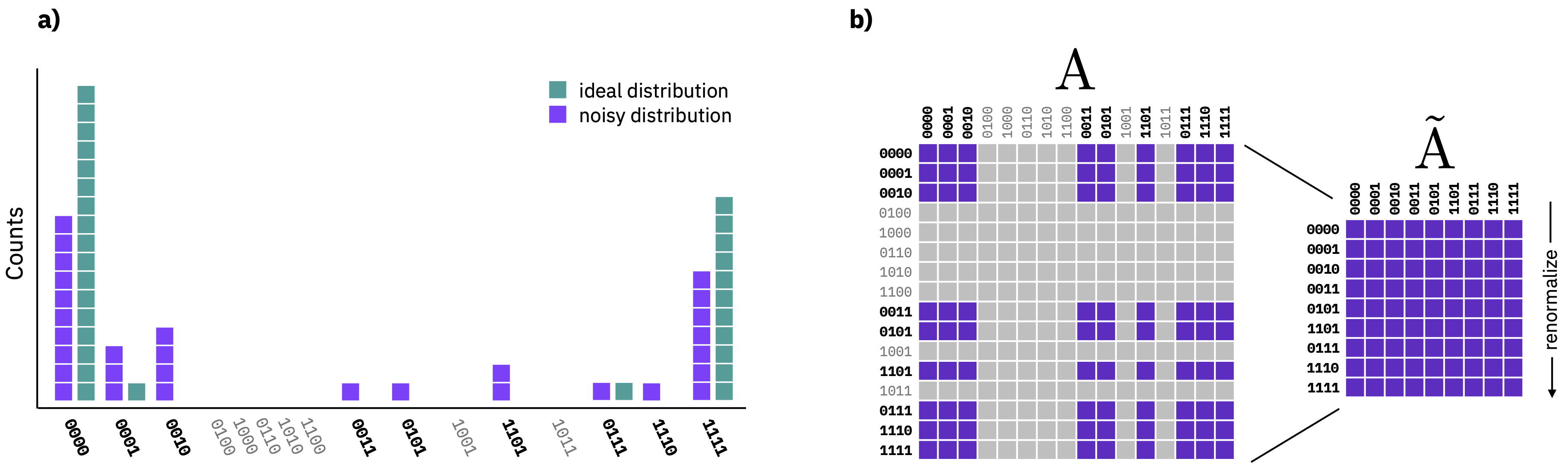
The rapid development and deployment of quantum computing systems has brought us ever closer to the goal of reaching quantum advantage; the point at which executing one of more tasks on a quantum computer provides tangible benefits over classical computation methods. However, at the same time, noise and errors in near-term quantum devices greatly limit their full potential. As such, researchers have developed several mitigation strategies to approximately cancel quantum gate and measurement errors and boost the fidelity of experiments executed on these systems. In many quantum computing architectures, measurement errors play an outsized role and their mitigation is essential to getting accurate results for many near-term applications and algorithms. To date, the mitigation of measurement errors has been greatly limited by the exponential scaling of current techniques with the number of measured qubits. This bottleneck limits the use of present-day measurement-mitigation strategies to just a handful of qubits and prevents them from being used at scales needed for quantum advantage and beyond.

In this work, we present a scalable way of mitigating quantum measurement errors that allows for the mitigation of errors on numbers of qubits that would otherwise be out of reach for even the largest of supercomputers using previous methods. To achieve this, we put forth a truncation scheme that reduces the exponential overhead down to a scaling that depends on the number of observed bit strings and can be readily solved using standard computational methods. Our method works for both uncorrelated and correlated errors and yields accurate error bounds. We then take this reduction a step further and create a matrix-free method iterative method that mitigates measurement errors and is both performant and memory efficient. The validity of the truncation technique is experimentally verified and we perform mitigation experiments out to numbers of qubits that are otherwise impractical to solve.

Motivation

At the time, IBM was introducing the “Runtime” that takes input quantum circuits and does all the transpilation (pre-processing), execution, and post-processing server side. This is complicated by the fact that some stages of this workflow do not scale well, and are computationally expensive. Readout mitigation is one-such example, where naive implementations scale exponentially with the number of measured qubits. However, readout mitigation is critical for getting good results for problems such as variational algorithms. As such, I thought that there should be a better way to to perform such mitigation, and allow for scaling it up to large numbers of qubits.

Possible Extensions

It is difficult to describe extensions to this work in few words. There are ways to combine M3 with other readout mitigation techniques such as the one called “TREX”. There are ways to probe for correlated readout errors as well, but they may not be of overall value if such errors are small in practice (like on IBM systems).

Graph View

Backlinks